67. Largest Rectangle in Histogram

Topic :

stack

Difficulty :

hard

Problem Link :

problem statement

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

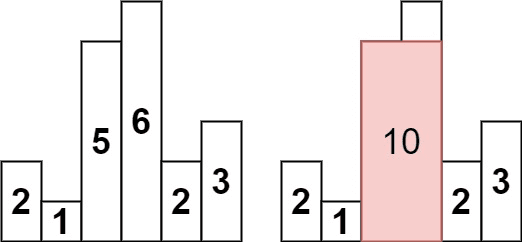
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.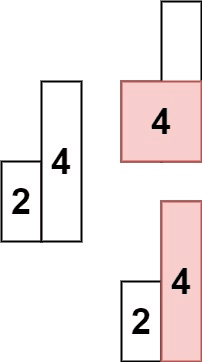

Example 2:

Input: heights = [2,4]
Output: 4

Constraints:

1 <= heights.length <= 105
0 <= heights[i] <= 104

solution

TIME COMPLEXITY : O(N)+O(N)+O(N) =O(3N)

SPACE COMPLEXITY:O(N)+O(N)+O(N) =O(3N)

import java.io.*;
import java.util.*;
class LargestRectangleInHistogram
{
 public static void main(String args[]){
     int []heights={2,1,5,6,2,3};
     System.out.println(largestRectangleArea(heights));
 }
 static int largestRectangleArea(int[] heights) {
      
      int[]previousSmallerHeights=new int[heights.length];
      int[]nextSmallerHeights=new int[heights.length];
      
      //fill the previous smaller heights array using the previous smaller concept
      Stack<Integer> stack=new Stack<>();
        
      for(int i=0;i<heights.length;i++){
         while(!stack.isEmpty() && heights[stack.peek()]>=heights[i])
             stack.pop();
         if(stack.isEmpty())
             previousSmallerHeights[i]=0;
          else
              previousSmallerHeights[i]=stack.peek()+1;
          
          stack.push(i);
      }
       
        stack.clear();
        
      //fill the next smaller heights using next smaller concept
      for(int i=heights.length-1;i>=0;i--){
          while(!stack.isEmpty() && heights[stack.peek()]>=heights[i])
              stack.pop();
          if(stack.isEmpty())
              nextSmallerHeights[i]=heights.length-1;
          else
              nextSmallerHeights[i]=stack.peek()-1;
          stack.push(i);
      }
        int maxArea=Integer.MIN_VALUE;
        for(int i=0;i<heights.length;i++){
            int left=previousSmallerHeights[i];
            int right=nextSmallerHeights[i];
            int area=heights[i]*(right-left+1);
                maxArea=Math.max(maxArea,area);
                
        }
        return maxArea;
        
    }
}