68. Maximal Rectangle

Topic :

stack

Difficulty :

hard

Problem Link :

problem statement

Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.

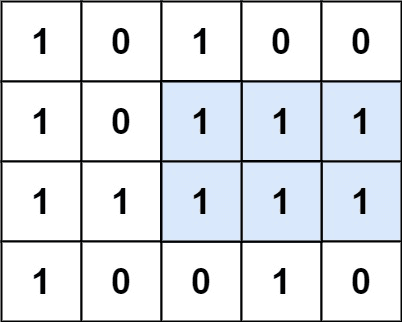
Example 1:

Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],
["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 6
Explanation: The maximal rectangle is shown in the above picture.

Example 2:

Input: matrix = [["0"]]
Output: 0

Example 3:

Input: matrix = [["1"]]
Output: 1

Constraints:

rows == matrix.length
cols == matrix[i].length
1 <= row, cols <= 200
matrix[i][j] is '0' or '1'.

solution

import java.io.*;
import java.util.*;
 class MaximalRectangle
{
  public static void main(String args[]){
    char matrix[][]={{'1','0','1','0','0'},
                    {'1','0','1','1','1'},
                    {'1','1','1','1','1'},
                    {'1','0','0','1','0'}};
    System.out.println(maximalRectangle(matrix));                
  }
  static int maximalRectangle(char[][] matrix) {
     int[]heights=new int[matrix[0].length];
        int area=0;
     for(int i=0;i<matrix.length;i++){
      for(int j=0;j<matrix[0].length;j++){
          if(matrix[i][j]=='1')
              heights[j]++;
          else
              heights[j]=0;
      }
        area=Math.max(area,largestAreaInHistogram(heights)); 
     }
      return area;
    }
    
  static int largestAreaInHistogram(int[] heights){
        
        int prev_smaller[]=new int[heights.length];
        int next_smaller[]=new int[heights.length];
        Stack<Integer> stack=new Stack<>();
        
        //find indexes of previous smaller heights
        for(int i=0;i<heights.length;i++){
            int currHeight=heights[i];
            while(!stack.isEmpty() && currHeight<=heights[stack.peek()])
                stack.pop();
            if(stack.isEmpty())
                prev_smaller[i]=0;
            else
                prev_smaller[i]=stack.peek()+1;
            stack.push(i);        
        }
        
        stack.clear();
        
        //find indexes of next smaller heights
        for(int i=heights.length-1;i>=0;i--){
            int currHeight=heights[i];
            while(!stack.isEmpty() && currHeight<=heights[stack.peek()])
                stack.pop();
            if(stack.isEmpty())
                next_smaller[i]=heights.length-1;
            else
                next_smaller[i]=stack.peek()-1;
            stack.push(i);        
        }
        
        int maxArea=0;
        for(int i=0;i<heights.length;i++){
            int right=next_smaller[i];
            int left=prev_smaller[i];
          int currArea=heights[i]*(right-left+1);
            maxArea=Math.max(currArea,maxArea);
        }
        return maxArea;
    }
}